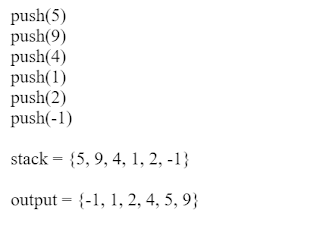CodeByAkram: Sorting Algorithm

Showing posts with label Sorting Algorithm. Show all posts

How to Sort a Stack using Merge Sort?

Interviewer may ask you this question if you have more than 3 years of experience in java development. So lets have a look, how to sort a stack using merge sort?

Lets see sample input and output for better understanding:

How to Sort a Stack using Merge Sort? codebyakram

Algorithm
For this we will follow these below two steps,
1. Break the stack into two parts by using two temporary stack.

2. When only one element remains on a Stack, Merge it.

Lets have a look on the program,

package com.codebyakram;
 
import java.util.Stack;
 
public class SortStack {
 
    public static void main(String args[]) {
        Stack stack = new Stack();
        stack.push(5);
        stack.push(9);
        stack.push(4);
        stack.push(1);
        stack.push(2);
        stack.push(-1);

 
        sort(stack);
 
        System.out.println(stack);
    }
 
    private static void sort(Stack stack) {
        Stack s1 = new Stack();
        Stack s2 = new Stack();
 
        while (stack.size() != 0) {
            if (stack.size() % 2 == 0) {
                s1.push(stack.pop());
            } else {
                s2.push(stack.pop());
            }
        }
 
        if (s1.size() > 1) {
            sort(s1);
        }
 
        if (s2.size() > 1) {
            sort(s2);
        }
 
        merge(s1, s2, stack);
    }
 
    private static void merge(Stack s1, Stack s2, Stack stack) {
        Stack mergedStack = new Stack();
        while (!s1.isEmpty() && !s2.isEmpty()) {
            if ((Integer) s1.peek() < (Integer) s2.peek()) {
                mergedStack.push(s2.pop());
            } else {
                mergedStack.push(s1.pop());
            }
        }
 
        while (!s1.isEmpty()) {
            mergedStack.push(s1.pop());
        }
 
        while (!s2.isEmpty()) {
            mergedStack.push(s2.pop());
        }
 
        while (!mergedStack.isEmpty()) {
            stack.push(mergedStack.pop());
        }
    }
}

Heap Sort in Java

Akram Interview Questions , Java

Before looking into Heap Sort, let's understand what is Heap and how it helps in sorting.
What is Complete Binary Tree?
A Complete binary tree is a binary tree in which every node other than the leaves has two children. In complete binary tree at every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

Let's understand with simple words now,
If a Binary Tree is filled level by level, left to right (Left child followed by Right child.) then it is called complete binary tree.

If Right child is present without Left child then it is not complete.

What is Heap property in Binary Tree?

A binary Tree is said to follow a heap property if tree is complete binary tree and every element of the tree is Larger (or Smaller) than any of its descendants if they exists.

Depending on the ordering, a heap is called a max-heap or a min-heap.
In a Max-heap, the keys of parent nodes are always greater than or equal to those of the children.
In max-heap, Largest element of the Tree is always at top(Root Node).

In a Min-heap, the keys of parent nodes are less than or equal to those of the children.
In min-heap, Smallest element of the Tree is always at top(Root Node).

Important aspects of Heap sort. (Prerequisites)
Before going into Heapsort algorithm, Let's understand few points,

If we have an array say [4, 10, 3, 5, 1], then we can represent array as complete binary tree
(start adding nodes from left to right) like shown below.

Each element has left and right child present in array except for leaf nodes, but how to find left and right child of non-leaf nodes in array.

We will get left and right child of non leaf elements using formula,
Left child index = 2 * (index of root, whose left and right child to find) + 1
Right child index = 2 * (index of root, whose left and right child to find) + 1

Left child and Right child of element at index 0 (element 4) is,
Left child index = 2 * i + 1 = 2 * 0 + 1 = 1
Right child index = 2 * i + 2 = 2 * 0 + 2 = 2

Left child and Right child of element at index 1 (element 10) is,
Left child index = 2 * i + 1 = 2 * 1 + 1 = 3
Right child index = 2 * i + 2 = 2 * 1 + 2 = 4

Left child and Right child of element at index 2 (element 3) is,
Left child index = 2 * i + 1 = 2 * 2 + 1 = 5
(index 5 is greater than length of array, so element 3 has no left child)

Right child index = 2 * i + 2 = 2 * 2 + 2 = 6
(index 6 is greater than length of array, so element 3 has no right child)

Algorithm
STEP 1: Logically, think the given array as Complete Binary Tree,

STEP 2: For sorting the array in ascending order, check whether the tree is satisfying Max-heap
property at each node,
(For descending order, Check whether the tree is satisfying Min-heap property)
Here we will be sorting in Ascending order,

STEP 3: If the tree is satisfying Max-heap property, then largest item is stored at the root of the heap.
(At this point we have found the largest element in array, Now if we place this element at
the end(nth position) of the array then 1 item in array is at proper place.)
We will remove the largest element from the heap and put at its proper place(nth position) in
array.

After removing the largest element, which element will take its place?
We will put last element of the heap at the vacant place. After placing the last element at the
root, The new tree formed may or may not satisfy max-heap property.
So, If it is not satisfying max-heap property then first task is to make changes to the tree, So
that it satisfies max-heap property.

(Heapify process: The process of making changes to tree so that it satisfies max-heap
property is called heapify)

When tree satisfies max-heap property, again largest item is stored at the root of the heap.
We will remove the largest element from the heap and put at its proper place(n-1 position) in
array.

Repeat step 3 until size of array is 1 (At this point all elements are sorted.)

Heapify Process with Example
Heapify process checks whether item at parent nodes has larger value than its left and right child.

If parent node is not largest compared to its left and right child, then it finds the largest item among parent, its left and right child and replaces largest with parent node.

It repeat the process for each node and at one point tree will start satisfying max-heap property.
At this point, stop heapify process and largest element will be at root node.

We found the largest element, Remove it and put it at its proper place in array,
Put the last element of the tree at the place we removed the node(that is at root of the tree)
Placing last node at the root may disturbed the max-heap property of root node.
So again repeat the Heapify process for root node. Continue heapify process until all nodes in tree satisfy max-heap property.

Initially, From which node we will start heapify process? Do we need to check each and every node that they satisfy heap property?
We do not have to look into leaf nodes as they don't have children and already satisfying max-heap property.
So, we will start looking from the node which has at least one child present.

How we will get that item in array, which has at least one child present?

By using the formula (array.length/2) - 1, we will be able to get the index of the item to start Heapify process.

Lets understand Heapify process with help of an example.

Heap Sort Java Program.

package com.codebyakram.sort;
 
public class HeapSort {
 
    public static void main(String[] args) {
        int[] array = new int[] {4, 10, 3, 5, 1};
 
        new HeapSort().sort(array);
 
        for (int i : array) {
            System.out.print(i + " ");
        }
    }
 
    public void sort(int data[]) {
        int size = data.length;
 
        /*
            {4, 10, 3, 5, 1}
 
                  4
                /  \
               10  3
              / \
             5  1
         */
        //This step is called building a Heap
        for (int i = size / 2 - 1; i >= 0; i--) {
            heapify(i, data, size);
        }
 
        //Once the heap is build by above step, we replace the max element at arr[0](root element) to last index of array
        //and decrease the size by 1 in next iteration as highest element is already at its place.
        for (int i = data.length - 1; i >= 0; i--) {
 
            //Swap max element at root(arr[0] to last element)
            int temp = data[0];
            data[0] = data[i];
            data[i] = temp;
 
            //reduce the heap window by 1
            size = size - 1;
 
            //swapping would have disturbed the heap property,
            //so calling max heapify for index 0 on the reduced heap size.
            //if we pass i in place of size should also work as that also represents the size
            heapify(0, data, size);
        }
    }
 
    private int leftChild(int i) {
        return 2 * i + 1;
    }
 
    private int rightChild(int i) {
        return 2 * i + 2;
    }
 
    private void heapify(int i, int[] data, int size) {
        int largestElementIndex = i;
 
        int leftChildIndex = leftChild(i);
        if (leftChildIndex < size && data[leftChildIndex] > data[largestElementIndex]) {
            largestElementIndex = leftChildIndex;
        }
 
        int rightChildIndex = rightChild(i);
        if (rightChildIndex < size && data[rightChildIndex] > data[largestElementIndex]) {
            largestElementIndex = rightChildIndex;
        }
 
        if (largestElementIndex != i) {
            int swap = data[i];
            data[i] = data[largestElementIndex];
            data[largestElementIndex] = swap;
 
            // Recursively heapify for the affected node
            heapify(largestElementIndex, data, size);
        }
    }
}

Summarize Heap Sort algorithm.
1. We build a heap(Max or Min) from the given array elements.
2. The root is the max (or min number). So extract it and put it in an array at its proper position.
3. Put last element at the root of the tree and Heapify the remaining elements.
4. Again extract the root and repeat heapification until there is one element in array.

Advantage of using Heap Sort algorithm for Sorting
1. Heap sort has the best possible worst case running time complexity of O(n Log n).
2. It doesn't need any extra storage and that makes it good for situations where array size is large.

Merge sort in Java

Akram Interview Questions , Java

Related questions: Sort Linked List using Merge Sort, Given a Linked list, Sort it using Merge Sort Algorithm.

Merge sort is preferred algorithm for sorting a linked list, lets see why,
The way linked list is structured which doesn't allow random access makes some other algorithms like Quicksort perform poorly, So Merge sort is often preferred algorithm for sorting linked list.

Lets understand what is the input and the expected output.

Algorithm (We will use Merge Sort for sorting Linked list.)
For sorting Linked list, we can use any algorithm but the most suitable algorithm is Merge Sort.

Why is merge sort preferred over quick sort for sorting linked lists?

As Singly Linked list can be accessed in only one direction and cannot be accessed randomly, Quick sort will not be well suitable here.

Quick sort requires access to elements in both direction for swapping and doing such operation in Linked list is not as easy as working with Arrays.
Starting from the end and moving backward is usually expensive operation in Singly linked list.
So Quick sort is well suited for arrays and not linked list.

Merge sort is a divide and conquer algorithm in which need of Random access to elements is less.
So Merge Sort can be used for sorting Linked list.

How Merge Sort works

Merge Sort works by breaking the linked list(or Array) into 2 equal parts say Left half and Right half.
Again break 2 list that we got in Step 1 in two equal parts each.
Repeat above steps until only 1 element remains in Linked list (or Array) because list with only 1 element is always sorted.
So in each step we are breaking the list in Left half and Right half.
When complete list is divided and contains only Single element in Left and Right half each, Start comparing and sorting each Left and Right half, So that portion of Linked list will be sorted.
Repeat Step 5 for all the remaining Left and Right half and complete linked list will be sorted.

It works on divide and conquer technique. Time complexity is O(N log N).

Lets understand with the help of below example.

Sorting Linked list using Merge sort in Java. (Recursive Approach)

package linkedlist.singly;
 
public class SortLinkedList {
 
 Node startNode;
  
 public static void main(String[] args) {
  new SortLinkedList();
 }
 
 public SortLinkedList() {
  Node node1 = new Node(10);
  Node node2 = new Node(1);
  Node node3 = new Node(-2);
  Node node4 = new Node(8);
  Node node5 = new Node(9);
  Node node6 = new Node(10);
  Node node7 = new Node(1);
 
  node1.setNext(node2);
  node2.setNext(node3);
  node3.setNext(node4);
  node4.setNext(node5);
  node5.setNext(node6);
  node6.setNext(node7);
 
  startNode = node1;
   
  Node sortedStartNode = mergeSortLinkList(startNode);
  printLinkList(sortedStartNode);
 }
 
 private Node mergeSortLinkList(Node startNode){
   
  //Break the list until list is null or only 1 element is present in List.
  if(startNode==null || startNode.getNext()==null){
   return startNode;
  }
 
  //Break the linklist into 2 list.
  //Finding Middle node and then breaking the Linled list in 2 parts.
  //Now 2 list are, 1st list from start to middle and 2nd list from middle+1 to last.
   
  Node middle = getMiddle(startNode);
  Node nextOfMiddle = middle.getNext();
  middle.setNext(null);
 
  //Again breaking the List until there is only 1 element in each list.
  Node left = mergeSortLinkList(startNode);
  Node right = mergeSortLinkList(nextOfMiddle);
 
  //Once complete list is divided and contains only single element, 
  //Start merging left and right half by sorting them and passing Sorted list further. 
  Node sortedList = mergeTwoListRecursive(left, right);
   
  return sortedList;
 }
 
 //Recursive Approach for Merging Two Sorted List
 private Node mergeTwoListRecursive(Node leftStart, Node rightStart){
  if(leftStart==null)
   return rightStart;
   
  if(rightStart==null)
   return leftStart;
 
  Node temp=null;
   
  if(leftStart.getData() < rightStart.getData()){
   temp=leftStart;
   temp.setNext(mergeTwoListRecursive(leftStart.getNext(), rightStart));
  }else{
   temp=rightStart;
   temp.setNext(mergeTwoListRecursive(leftStart, rightStart.getNext()));
  }
  return temp;
 }
 
 private Node getMiddle(Node startNode) {
  if(startNode==null){
   return startNode;
  }
 
  Node pointer1=startNode;
  Node pointer2=startNode;
   
  while(pointer2!=null && pointer2.getNext()!=null && pointer2.getNext().getNext()!=null){
   pointer1 = pointer1.getNext();
   pointer2 = pointer2.getNext().getNext();
 
  }
  return pointer1;
 }
 
 private void printLinkList(Node startNode) {
  Node temp = startNode;
  while(temp!=null){
   System.out.print(temp.getData() + " ");
   temp = temp.getNext();
  }
 }
  
}

Sorting Linked list using Merge sort in Java. (Iterative Approach)

package linkedlist.singly;
 
public class SortLinkedList {
 
 Node startNode;
 
 public static void main(String[] args) {
  new SortLinkedList();
 }
 
 public SortLinkedList() {
  Node node1 = new Node(10);
  Node node2 = new Node(1);
  Node node3 = new Node(-2);
  Node node4 = new Node(8);
  Node node5 = new Node(9);
  Node node6 = new Node(10);
  Node node7 = new Node(1);
 
  node1.setNext(node2);
  node2.setNext(node3);
  node3.setNext(node4);
  node4.setNext(node5);
  node5.setNext(node6);
  node6.setNext(node7);
 
  startNode = node1;
 
  Node sortedStartNode = mergeSortLinkList(startNode);
  printLinkList(sortedStartNode);
 }
 
 private Node mergeSortLinkList(Node startNode){
 
  //Break the list until list is null or only 1 element is present in List.
  if(startNode==null || startNode.getNext()==null){
   return startNode;
  }
 
  //Break the linklist into 2 list.
  //Finding Middle node and then breaking the Linled list in 2 parts.
  //Now 2 list are, 1st list from start to middle and 2nd list from middle+1 to last.
 
  Node middle = getMiddle(startNode);
  Node nextOfMiddle = middle.getNext();
  middle.setNext(null);
 
  //Again breaking the List until there is only 1 element in each list.
  Node left = mergeSortLinkList(startNode);
  Node right = mergeSortLinkList(nextOfMiddle);
 
  //Once complete list is divided and contains only single element, 
  //Start merging left and right half by sorting them and passing Sorted list further. 
  Node sortedList = mergeTwoListIterative(left, right);
 
  return sortedList;
 }
 
 //Iterative Approach for Merging Two Sorted List
 private Node mergeTwoListIterative(Node leftStart, Node rightStart) {
 
  Node merged=null;
  Node temp=null;
 
  //To keep track of last element, so that we don't need to iterate for adding the element at last of 
  //list when either LeftStart or rightStart is NULL.
  Node lastAddedNode = null;
 
  while(leftStart!=null && rightStart!=null){
 
   if(leftStart.getData()>rightStart.getData()){
    temp = new Node(rightStart.getData());
    rightStart=rightStart.getNext();
 
   }else{
    temp = new Node(leftStart.getData());
    leftStart=leftStart.getNext();
   }
 
   if(merged==null){
    merged=temp;
   }else{
    lastAddedNode.setNext(temp);     
   }
   lastAddedNode=temp;
  }
 
  if(leftStart!=null){
   lastAddedNode.setNext(leftStart);
  }else{
   lastAddedNode.setNext(rightStart);
  }
   
  return merged;
 }
 
 private Node getMiddle(Node startNode) {
  if(startNode==null){
   return startNode;
  }
 
  Node pointer1=startNode;
  Node pointer2=startNode;
 
  while(pointer2!=null && pointer2.getNext()!=null && pointer2.getNext().getNext()!=null){
   pointer1 = pointer1.getNext();
   pointer2 = pointer2.getNext().getNext();
 
  }
  return pointer1;
 }
 
 private void printLinkList(Node startNode) {
  Node temp = startNode;
  while(temp!=null){
   System.out.print(temp.getData() + " ");
   temp = temp.getNext();
  }
 }
 
}

Insertion Sort in Java

Akram Interview Questions , Java

Given a array of integers, Sort it using Insertion sort.
Lets understand what is the input and the expected output.

Example
Assume 5 persons of different heights are visiting at your office each at 5 minutes interval and you need to make them stand according to their heights(smaller to higher). How you will do?

Below is the sequence in which person is going to visit you,

You need to arrange above persons based on their height.
First "A" will visit and that is the only person present, so just tell him to stand and you don't need to take any decision.

Second "B" will visit, so now you have to compare "B" height with "A" height, which is smaller, so shift "A" one step back and move "B" one step ahead.
Now, you have arranged 2 persons properly.

Now "C" entered in office, so you have to find proper position for "C" to stand.
First you will compare "C" height with "A", which is smaller so "A" need to be shifted one step back and "C" need to be shifted one step in front.
Now, compare "C" height with "B", which is higher than "B", So stop here because you have found proper position of "C" to stand.
Now, you have arranged 3 persons properly.

Now "E" entered in office, so you have to find proper position for "E" to stand.
First you will compare "E" height with "D", which is smaller so "D" need to be shifted one step back and "E" need to be shifted one step in front.
Now compare "E" height with "A", which is smaller so "A" need to be shifted one step back and "E" need to be shifted one step in front.
Now compare "E" height with "C", which is smaller so "C" need to be shifted one step back and "E" need to be shifted one step in front.
Now, compare "E" height with "B", which is higher than "B", So stop here because we have found proper position of "E" to stand and all the person ahead of B will be smaller than "B", so no need to check further.

Same logic we will use in Insertion sort.
Algorithm
Insertion Sort is very basic and easy sorting algorithm to understand and implement.

Insertion sort works by shifting and putting element at its correct position in array.

Lets see how it works:

Insertion sort start's sorting an array by picking 1st element of array.
(We begin by assuming that a array with one item (position 0) is already sorted.)
So now we have one sorted elements set.

Now, we will pick 2nd element of array and compare it with sorted elements set one by one until we find correct position of 2nd element in sorted set.
Elements which are higher than 2nd element are shifted one step back to make space for 2nd element.
After putting 2nd element at its correct position, we have 2 elements in our sorted set.

Now, we will pick 3rd element of array and compare it with sorted elements set one by one until we find correct position of 3rd element in sorted set.
Elements which are higher than 3rd element are shifted one step back to make space for 3rd element.
After putting 3rd element at its correct position, we have 3 elements in our sorted set.

Repeat the process until all elements are sorted.

Complexity
1. The insertion sort, unlike the other sorts, passes through the array only once.
2. The insertion sort splits an array into two sub-arrays,
First sub-array on left side is always sorted and increases in size as the sort continues.
Second sub-array is unsorted, contains all the elements yet to be inserted into the first sub-array,
and decreases in size as the sort continues.

3. Insertion sort is efficient for (quite) small data sets.
4. It is more efficient than selection sort or bubble sort.
5. Insertion sort is very efficient for arrays which is nearly(almost) sorted and it sorts nearly sorted
array in time complexity of O(N).
(For sorting an array containing elements in descending order to ascending order, insertion sort
will give poor performance and complexity will be O(N^2))

6. It is Stable sort; i.e., does not change the relative order of elements with equal keys.
7. It is In-place sort; i.e., only requires a constant amount O(1) of additional memory space
8. It can sort elements as it receives it and no need of complete data initially before start sorting.
(Online).
Java Program for Insertion Sort

package sorting;
 
public class InsertionSort {
 public static void main(String[] args) {
  new InsertionSort();
 }
 
 public InsertionSort() {
  int[] arr=new int[]{1,9,4,10,0};
 
  System.out.println("Before Sorting...");
  printArray(arr);
   
  insertionSort(arr);
   
  System.out.println("\nAfter Sorting...");
  printArray(arr);
 }
 
 private void insertionSort(int arr[]){
  if(arr==null || arr.length<2){
   return;
  }
 
  for (int i = 1; i < arr.length; i++) {
   int temp = arr[i];
    
   // Comparison starts from one step back of element on which we are working that is i.
   int j=i-1; 
    
   //Compare elements till we not found element higher than temp or all element are compared.
   while( j >= 0 && arr[j] > temp){
    arr[j+1] = arr[j];
    j--;
   }
   arr[j+1]=temp;   
  }
 }
 
 private void printArray(int arr[]){
  for (int i = 0; i < arr.length; i++) {
   System.out.print(arr[i] + " ");
  }
 }
  
}

Selection Sort in Java

Akram Interview Questions , Sorting Algorithm

Selection Sort in Java

The selection sort is the improvement over bubble sort by making only one exchange for every pass through the list.

In this algorithm, find the smallest element from an unsorted list in each iteration and place that element at beginning of the list.

Or find the largest element from an unsorted list in each iteration and place that element at the end of the list.

How Selection Sort Works?

1. Lets take and list as mentioned below and take the first element as minimum

2. Compare first element with the second element is the second element is smaller than first then assign second element to minimum. Compare minimum with the third element and if the third element is smaller than minimum then assign thirst variable to minimum. The process goes on until the last element.

3. After each iteration, minimum placed at the beginning of unsorted list by swapping.

4. For each iteration, indexing start from the first unsorted element. Step 1 and 3 are repeated until all the elements are placed at their correct positions.

5. And the selection is sort all the elements by using above steps in recursive method.

 // Selection sort in Java
import java.util.Scanner;
class SelectionSort {
  void selectionSort(int array[]) {
    int size = array.length;
    for (int step = 0; step < size - 1; step++) {
      int min_idx = step;
      for (int i = step + 1; i < size; i++) {
        if (array[i] < array[min_idx]) {
          min_idx = i;
        }
      }
      int temp = array[step];
      array[step] = array[min_idx];
      array[min_idx] = temp;
    }
  }
  void printArray(int array[]) {
    int size = array.length;
    for (int i = 0; i < size; ++i)
      System.out.print(array[i] + " ");
    System.out.println();
  }
  public static void main(String args[]) {
    int[] data = { 20, 12, 10, 15, 2 };
    SelectionSort ss = new SelectionSort();
    ss.selectionSort(data);
    System.out.println("Sorted Array in Ascending Order: ");
    ss.printArray(data);
  }
}

Complexity

Now lets talk about the complexity of selection sort.

Complexity = O(n2)

Also, we can analyze the complexity by simply observing the number of loops. There are 2 loops so the complexity is O(n*n) = O(n²). So the complexity of this algorithm is O(n*n) = O(n2 ). This is the worst case complexity.

Where we can use bubble sort?

The selection sort is used when:

1. small list is to be sorted

2. cost of swapping does not matter

3. checking of all the elements is compulsory

4. cost of writing to a memory matters like in flash memory (number of writes/swaps is O(n) as compared to O(n2) of bubble sort)

Bubble Sort

Akram Interview Questions , Sorting Algorithm

Bubble Sort

The bubble sort makes multiple passes through a list and sometimes referred to as sinking sort. It is a simple sorting algorithm that compare the adjacent elements and swap their position if they are nor in intended order. Each pass through the list places the next largest value in its proper place. In essence, each item “bubbles” up to the location where it belongs.

So now lets talk about How Bubble sort works?

Lets take an list as shown below

As Shown above, Starting from the first element, two adjacent elements are compared. If the former element is greater than the latter one, they are swapped. This process goes on for all consecutive-element pairs until the last unsorted element.

And again it will follow the same recursive method till the complete list is sorted.

class BubbleSort{

  public void bubbleSort(int array[]){

    int size = array.length;

    for (int i = 0; i < size-1; i++){

      for (int j = 0; j < size-i-1; j++){

        if (array[j] > array[j+1]){

          int temp = array[j];

          array[j] = array[j+1];

          array[j+1] = temp;

        }

      }

    }

  }

  Public void printArray(int array[]){

    int size = array.length;

    for(int i=0; i < size; ++i)

      System.out.print(array[i]+" ");

      System.out.println();

  }

  public static void main(String args[]){

  int[] data = {-2, 45, 0, 11, -9};

  BubbleSort bs = new BubbleSort();

  bs.bubbleSort(data);

  System.out.println("Sorted Array in Ascending Order:");

  bs.printArray(data);

  }

}

Complexity

Now lets talk about the complexity of bubble sort.

As Bubble sort is the simplest sorting algorithm and in above java code we have implemented two foor loops, So the complexity of of this algorithm is O(n*n) = O(n²). This is the worst case complexity.

Where we can use bubble sort?

1. Where the complexity of code does not matters

Where a sort code is refer.

How to Sort a Stack using Merge Sort?

Heap Sort in Java

Merge sort in Java

Insertion Sort in Java

Selection Sort in Java

How Selection Sort Works?

Bubble Sort

Search This Blog

Popular

Categories

Blog Archive

Tags

Popular Posts